스패닝 트리
스패닝 트리
어떤 무향 그래프의 스패닝 트리는 원래 그래프의 정점 전부와 간선의 부분 집합으로 구성된 부분 그래프이다.
스패닝 트리에 포함된 간선들은 정점들을 트리 형태로 전부 연결해야하는데, 이는 사이클이 없고 정점들이 꼭 부모-자식 관계로 연결될 필요는 없다는걸 의미한다.
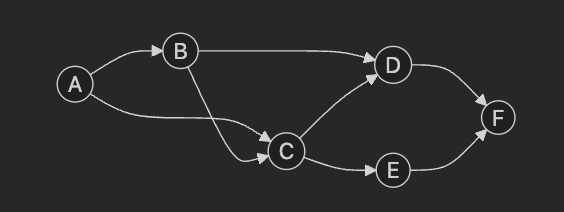 예시 그래프
예시 그래프
위의 예시 그래프에서 스패닝 트리를 그려보자. 스패닝 트리는 유일하지 않을 수 있다.
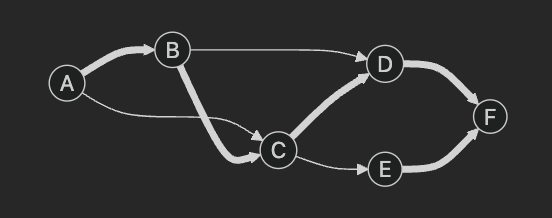 _올바른 스패닝 트리 1 _
_올바른 스패닝 트리 1 _
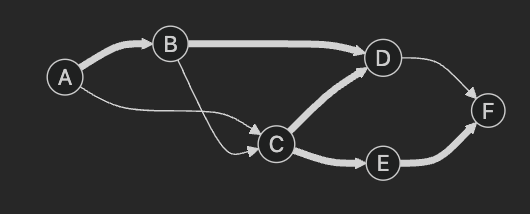 올바른 스패닝 트리 2
올바른 스패닝 트리 2
스패닝 트리는 모든 정점이 연결되어 있거나, 사이클이 있으면 안된다.
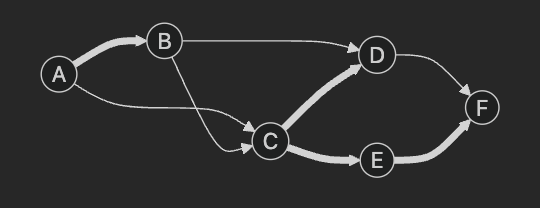 잘못된 스패닝 트리 1 (모든 정점이 연결되어 있지 않음)
잘못된 스패닝 트리 1 (모든 정점이 연결되어 있지 않음)
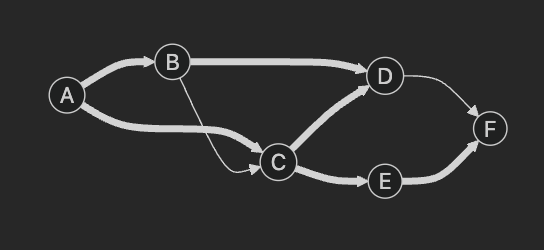 잘못된 스패닝 트리 2 (모든 정점이 연결되어 있지만 사이클이 존재)
잘못된 스패닝 트리 2 (모든 정점이 연결되어 있지만 사이클이 존재)
최소 스패닝 트리
가중치가 있는 그래프에서, 스패닝 트리 중 가중치의 합이 가장 작은 트리를 최소 스패닝 트리라고 한다.
최소 스패닝 트리를 찾는 알고리즘에는 크게 두 가지가 존재한다.
- 크루스칼
- 프림
두 알고리즘은 모두 간선이 하나도 없는 상태 에서 시작해 하나씩 트리에 가중치가 가장 작은 간선을 추가해 가는 그리디 알고리즘 으로, 접근 방법이 달라보이지만 같은 방법으로 증명할 수 있다는 특징도 있다.
크루스칼 알고리즘
크루스칼의 기본적인 아이디어는 가중치가 작은 간선이 최소 스패닝 트리에 포함될 가능성이 높다 이다.
그래서
- 모든 간선의 가중치를 오름차순으로 정렬한다
- 가중치가 작은 순서대로 스패닝 트리에 추가한다.
- 단, 스패닝 트리에 사이클이 생기지 않도록 한다
이런 방식으로 모든 간선을 한 번씩 검사하고 나면 크루스칼 알고리즘은 종료된다.
알고리즘 동작 방식
이제 예시를 들어, 한 번 직접 진행해보자.
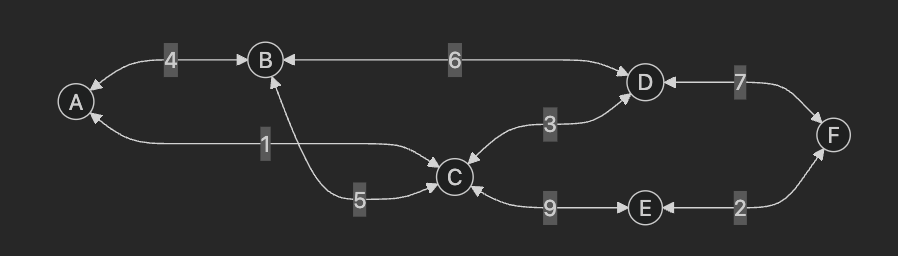 크루스칼 알고리즘의 예시 1
크루스칼 알고리즘의 예시 1
우선 가중치들을 정렬하면 [1, 2, 3, 4, 5, 6, 7, 9] 가 될 것이다.
- 가중치가 가장 작은 A - C (1) 을 선택해보자.
처음 뽑는 간선이다보니 당연히 사이클은 그려지지 않을 것이다.
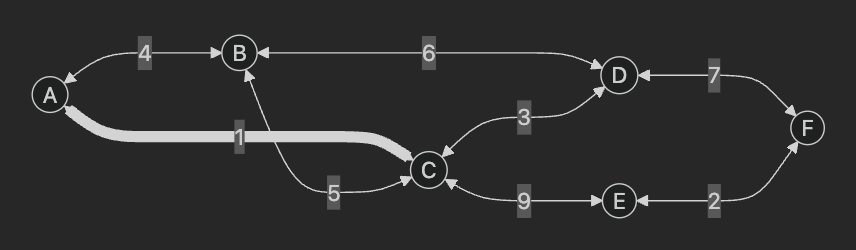 가중치가 1인 A - C 선택
가중치가 1인 A - C 선택
- 두 번째로 작은 E - F (2) 를 선택하자.
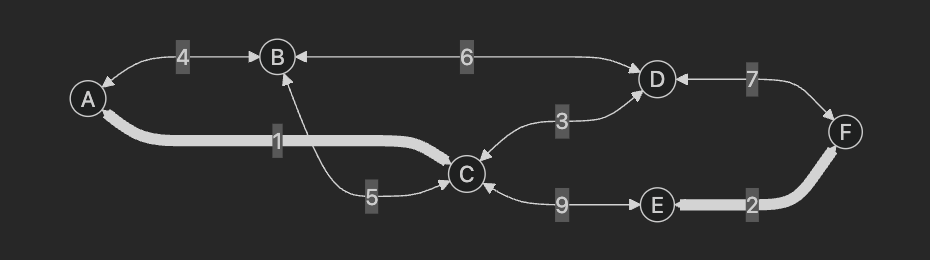 가중치가 2인 E - F 산텍
가중치가 2인 E - F 산텍
- 마찬가지로, C - D (3) 과 A - B (4) 를 선택해보자
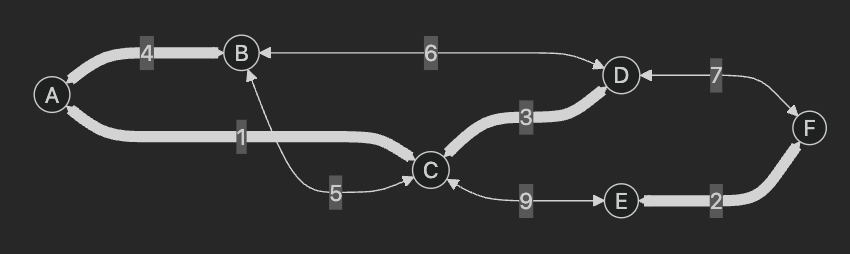 가중치가 3인 C - D, 가중치가 4인 A - B 선택
가중치가 3인 C - D, 가중치가 4인 A - B 선택
- 이제 남은 간선중에 가중치가 가장 작은 B - C (5) 를 선택하려고 보니, A - B - C 간의 사이클이 발생한다. 마찬가지로 그 다음 가중치가 작은 B - D (6) 을 선택하면 A - B - D -C 간의 사이클이 발생한다.
- 사이클이 생기지 않는 선에서 가장 작은 가중치를 갖는 D - F (7) 을 연결한다.
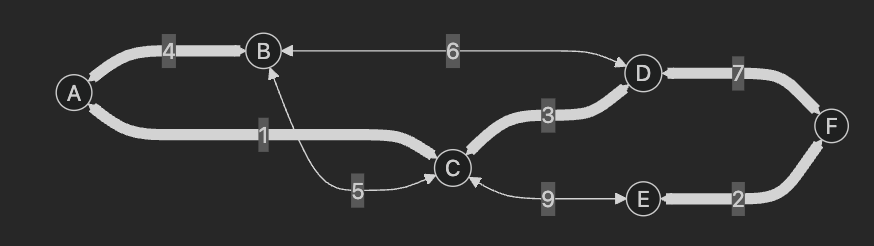 가중치가 7인 D - F 선택
가중치가 7인 D - F 선택
- C - E 도 마찬가지로 사이클이 생기기 때문에 선택하지 않는다.
- 모든 간선에 대해 검사를 완료했으므로 종료한다.
사이클 검사 방법
알고리즘 동작 방식을 봤을 때, 딱히 어려울 게 없어 보이는 단순한 방식으로 보인다.
다만 사이클이 생기는지 확인하는 작업을 어떻게 하는지를 고민해봐야 할 것 같다.
- DFS
결국 스패닝 트리 이므로 트리에 간선을 추가한 뒤에, 이 간선의 역방향 간선이 존재하는지를 DFS 로 탐색하면 어떨까?
예를 들어 A - B (4) 를 스패닝 트리에 추가하고 모든 간선마다 DFS 를 수행한다.
방문 기록을 저장해두면서 DFS 를 타고가다가, 이미 방문했던 곳을 방문한다면 사이클이 생긴 것이다.
이 과정을 간선을 추가할 때 마다 진행하면 된다.
이 방법은 구현하기에 매우 간단하겠지만 시간 복잡도를 생각해봤을 때, DFS 의 시간복잡도인 O(V+E) 에 E 를 곱한, O(E^2) 가 된다.
- Union-Find
두 정점을 잇는 간선에서, 이 간선이 사이클을 만들어내는지 확인하려면 두 정점이 같은 그룹에 있는지 확인하면 된다. 그리고 같은 그룹이 아니라면, 간선을 추가하면서 같은 그룹으로 만들어주는 작업을 반복하면 사이클 검사를 쉽게 할 수 있다.
이러한 자료구조를 만족하는 Union-Find 를 활용하면 쉽게 사이클을 검사할 수 있을 것 같다.
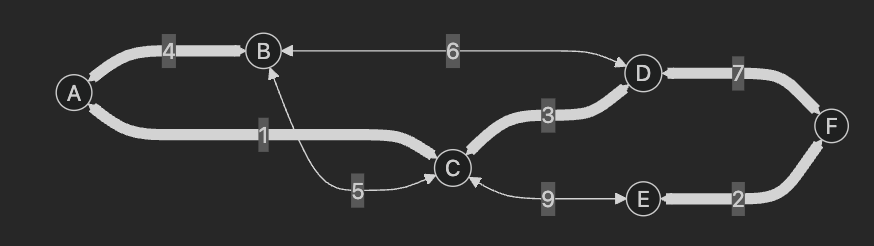 Union-Find 사이클 탐색 예시
Union-Find 사이클 탐색 예시
예를 들어, 가중치가 1인 A - C 를 검사해보자.
초기화단계에서는 A부터 F까지 어디에도 연결되지 않은 상태이므로, 당연히 자기 자신을 부모노드로 가진 채 초기화되어있을 것이다.
그렇기 때문에 A 와 C 는 같은 집합에 존재하지 않기 때문에 사이클이 생기지 않는다고 확신할 수 있다.
이후에 C 의 부모 노드를 A 로 바꾸면서 같은 집합으로 만들어준다.
이어서 E - F (2) 도 Union 하고 나서 C - D(3) 를 보자.
C 의 부모노드는 이미 A 이고, D 의 부모노드는 자신(D) 이다.
둘이 같은 집합이 아니므로 D의 부모노드를 A로 바꾼다.
A - B 도 마찬가지로, B의 부모노드가 A 로 바뀐다.
이제 가중치가 5인 B - C 를 추가할지 말지 결정해야한다.
B와 C의 루트노드를 살펴보니 전부 다 A 인 것을 알 수 있다.
따라서 사이클이 생길 수 있는 간선이므로 추가하지 않는다.
시간 복잡도
Union-Find 연산은 현실적으로 매우 짧은 시간(상수 시간)으로 봐도 되기 때문에 실제 트리를 만드는 for 문의 시간 복잡도는 O(E) 라고 봐도 좋다.
간선 리스트의 정렬에 걸리는 시간은 O(ElogE) 이기 때문에 O(ElogE) 가 전체 시간 복잡도가 된다.
증명
크루스칼 알고리즘은 각 간선을 그래프에 추가할 때, 뒤에 오는 간선들에 대한 고려는 전혀 하지 않으므로 탐욕적 알고리즘으로 분류할 수 있다.
따라서,
- 탐욕적 선택 속성은 우리가 내리는 탐욕적인 선택으로 인해 손해를 볼 일이 없음을 증명해야한다.
- 항상 최적의 선택만을 내려도 전체 문제의 최적해를 얻을 수 있어야 한다.
이렇게 두 가지의 증명을 함으로서 크루스칼 알고리즘의 정당성을 증명할 수 있다.
- 가장 짧은 간선을 선택해도 손해를 볼 일이 없다.
이 증명은 귀류법으로 할 수 있다.
크루스칼 알고리즘이 선택한 간선 루트가 올바르지 않다고 가정을 해보자.
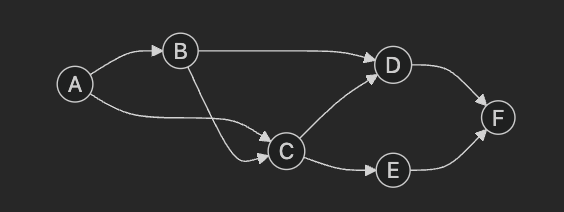 예시 그래프
예시 그래프
크루스칼 알고리즘은 A → B → C → D → F → E 를 최선으로 골랐는데, 실제로는 A → B → C → E → F → D 였다고 가정해보자.
크루스칼은 C - D 간선을 선택했지만 실제로는 C - D 간선이 아니라 C - E 간선을 선택해야 최소 스패닝 트리라는 것이다.
크루스칼은 항상 가중치의 최솟값부터 선택해나간다. 따라서 C - D 의 가중치가 C - E 보다 작기 때문에 크루스칼 알고리즘이 C - D 를 선택했을 것이다.
그렇다면 만약에 C - E 간선을 제거하고, C - D 간선을 연결하면 어떻게 될까? 이 또한 스패닝 트리가 되는 것을 알 수 있다. 따라서 가중치가 더 작은 간선을 선택해서 스패닝트리를 만들 수 있으므로, 처음의 A → B → C → E → F → D 가 최소 스패닝 트리라는 가정에서 모순 된다.
일반화를 시키자면, 실제 최소 스패닝트리 T 에 속하지 않으면서 크루스칼 알고리즘이 선택한 간선을 (u, v) 라고 하자. T 또한 스패닝 트리이므로 u 와 v 는 어떤 식으로든 연결이 되어 있을 것이다. 크루스칼 알고리즘은 최솟값부터 선택해나가므로 T에는 존재하지만 크루스칼이 선택하지 않은 간선 (a, b) 는 (u, v) 보다 무조건 가중치가 같거나 높을 수 밖에 없다. (a, b) 가 (u, v) 보다 가중치가 낮았다면 크루스칼은 (u, v) 가 아니라 (a, b) 를 선택했을 것이다.
이제 T 에서 u 와 v 를 잇는 경로 상의 어떠한 간선 하나를 제거하고, (u, v) 간선을 선택해보자. 이 때 간선 하나를 없앴지만 (u, v) 간선이 생겼으므로 스패닝 트리가 유지됨을 알 수 있고, 같거나 더 짧은 간선을 선택하면서 스패닝트리를 유지할 수 있으므로 T가 최소 스패닝 트리라는 가정에 모순이 생긴다.
- 항상 최적의 선택(남은 간선 중에, 사이클이 생기지 않는 가장 짧은 간선을 선택)만을 내려도 전체 문제의 최적해를 얻을 수 있어야 한다.
이는, 매 단계마다 선택되는 간선이 항상 최적의 부분 문제 해를 만족한다는 점에서 최적 부분 구조가 성립함을 쉽게 알 수 있다.
매 단계마다 선택하는 가장 짧은 간선은, 그 간선이 만드는 그래프 자체를 가장 짧은 경로로 갈 수 있게 한다. 따라서 항상 최적의 부분 문제 해를 만족하고 있다.
프림 알고리즘
크루스칼 알고리즘은 어느 간선이든 최솟값이면 선택하지만 프림 알고리즘은 현재 만들어진 트리에 이어진 간선만을 선택해나가면서 스패닝 트리를 만들게 된다.
프림 알고리즘도 트리에 이어진 간선 중에서 최솟값을 선택하기 때문에 크루스칼 알고리즘과 비슷하기도 하다.
그런데 이런 과정을 어딘가에서 많이 본 것 같다.
정점을 추가하면서, 정점에 연결된 간선 중에서 가장 짧은 간선을 선택해나가는 방식
이 방식은 다익스트라 알고리즘과 상당히 유사해보인다.
알고리즘 동작 방식
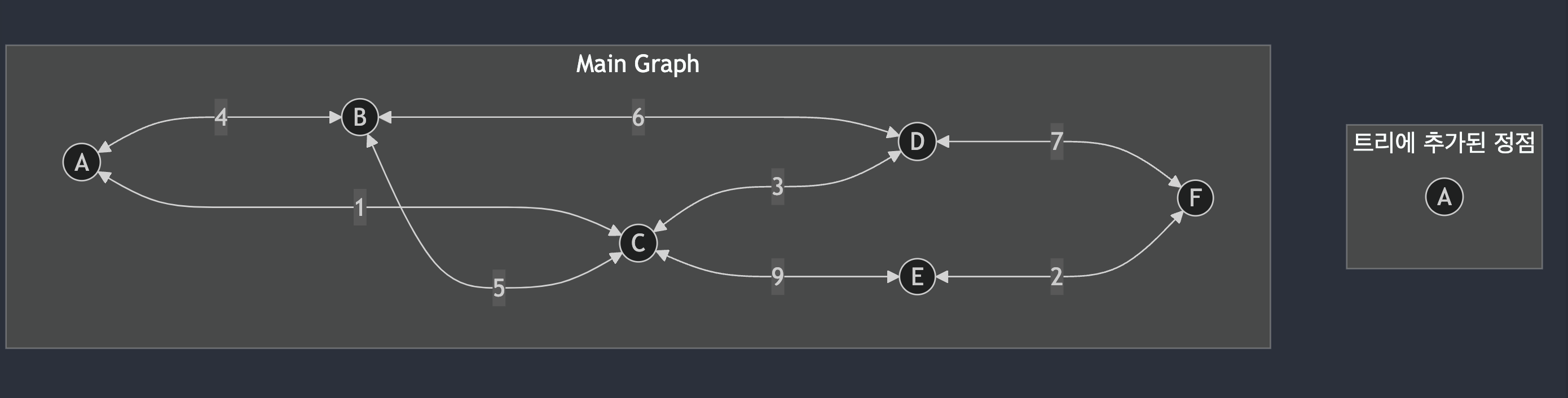 프림 알고리즘 예시 1
프림 알고리즘 예시 1
위의 그래프로 동작 방식을 한 번 살펴보자. 시작점은 A 라고 해보자.
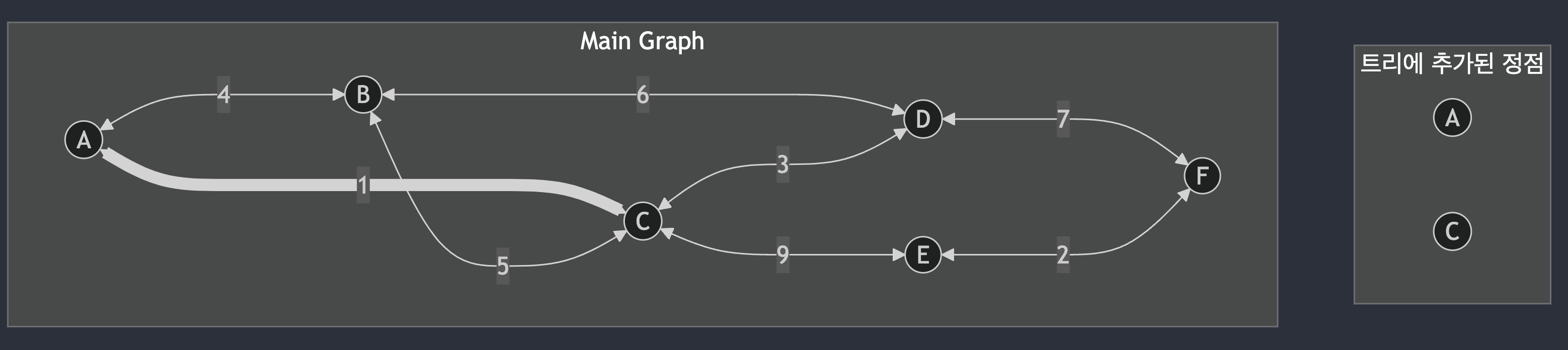 A - C 간선, 정점 C 추가
A - C 간선, 정점 C 추가
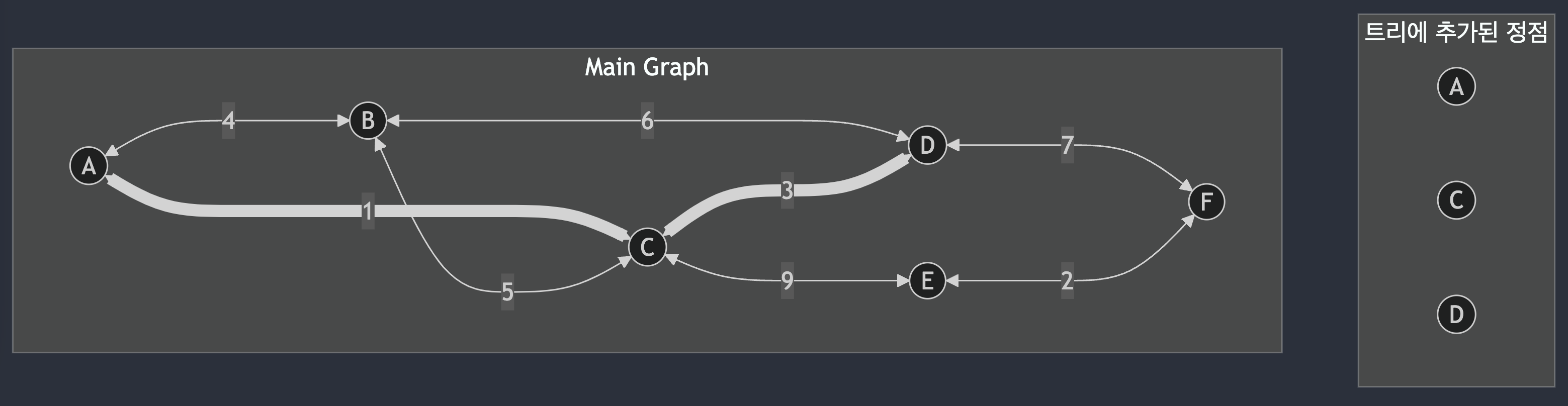 C - D 간선, 정점 D 추가
C - D 간선, 정점 D 추가
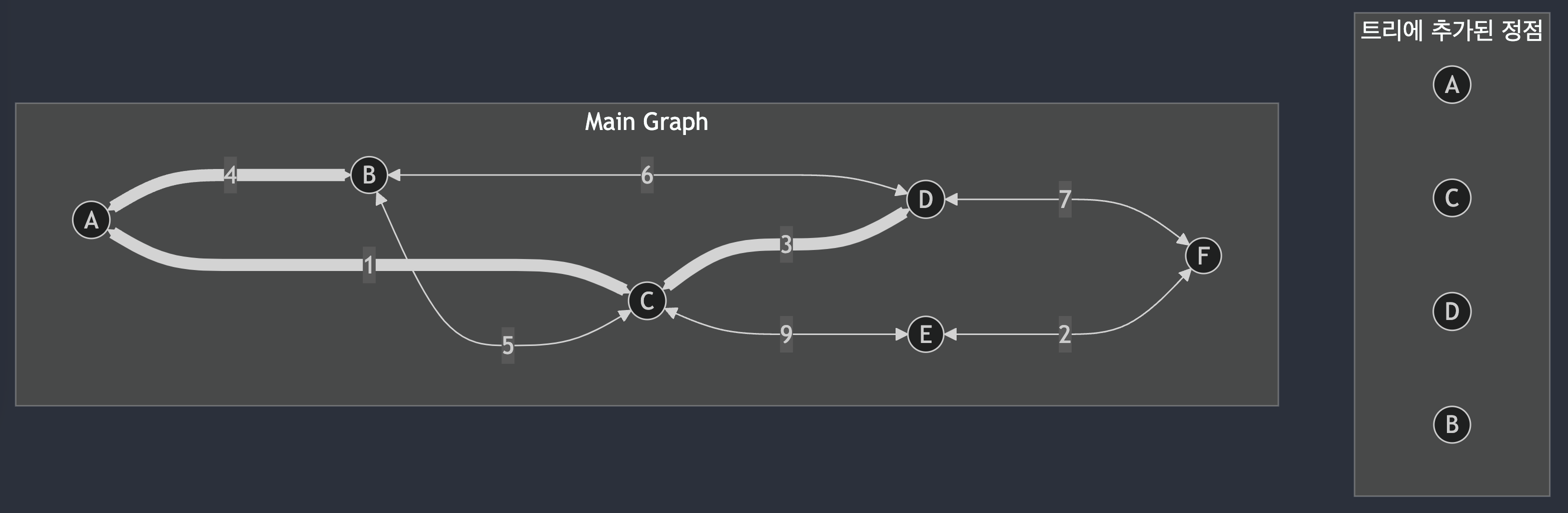 A - B 간선, 정점 B 추가
A - B 간선, 정점 B 추가
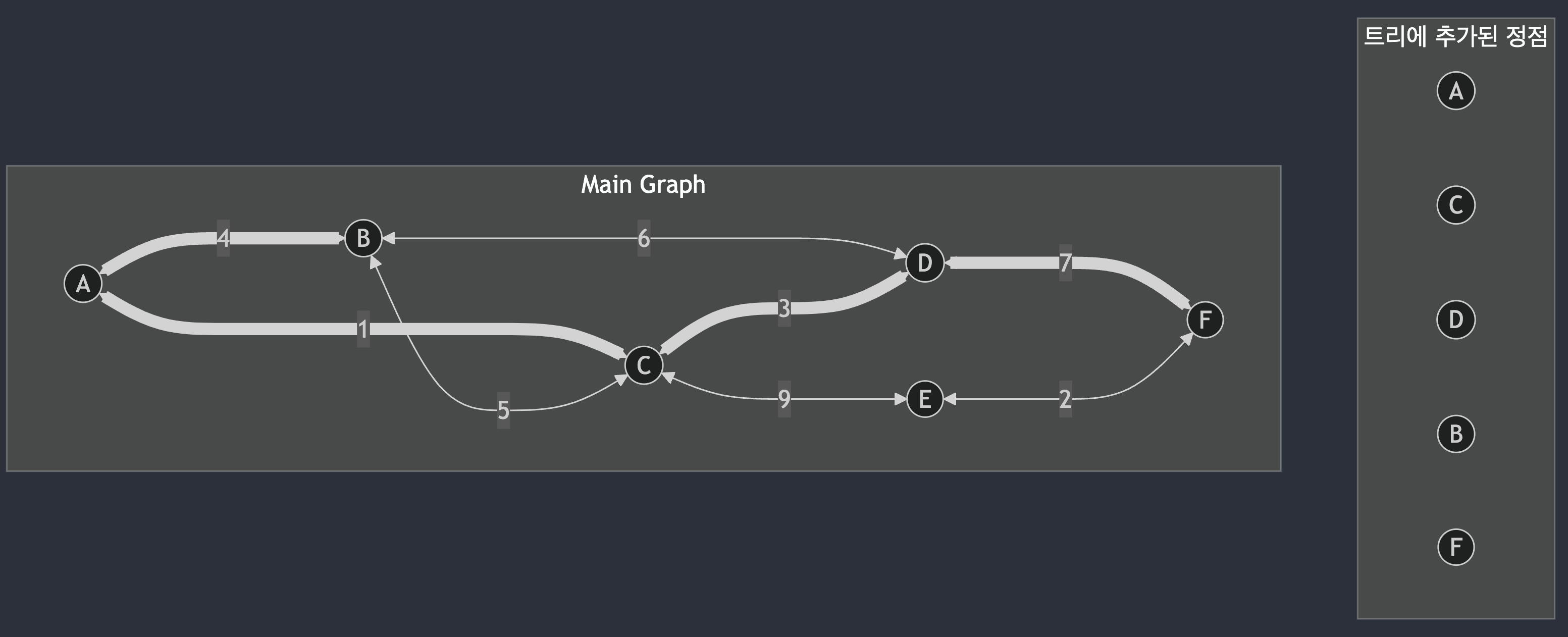 D - F 간선, 정점 F 추가
D - F 간선, 정점 F 추가
여기서 왜, 더 짧은 간선인 B - C(5), B - D(6) 을 선택하지 않았냐면 이미 정점 리스트에 들어가있는 C 와 D 를 잇는 간선이기 때문이다.
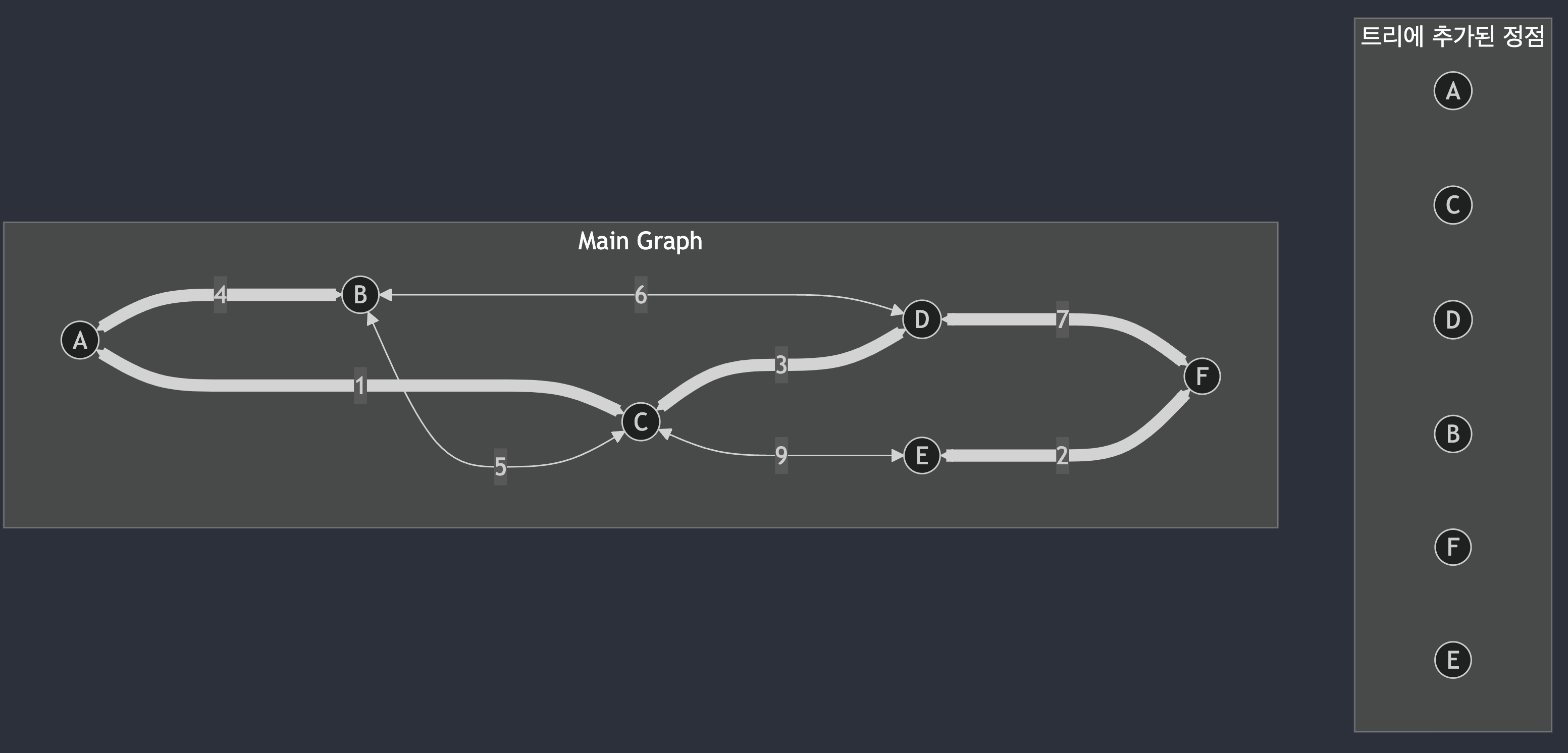 E - F 간선, 정점 E 추가
E - F 간선, 정점 E 추가
증명
프림 알고리즘은 크루스칼 알고리즘과 동일하게 간선의 최솟값을 사용하므로 증명이 크루스칼 알고리즘과 똑같다.
Subscribe to hoeeeeeh
Get the latest posts delivered right to your inbox